衡量相似性的方法

保持距离！

相似性

对于深度学习的各种任务，我们常常需要最小化模型输出与真实标签之间的距离，我们往往采用均方误差，交叉熵等作为损失函数，换句话说，不管是拉近它们分布之间的距离，还是什么，都是在使它们这两个张量更为相似。因此我们任何能衡量两组数据的相似性的方法都可以作为损失函数。这里总结一下各种计算相似度的方法。

余弦相似度

余弦相似性通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。

计算方式：

两个向量间的余弦值可以通过使用欧几里得点积公式求出：

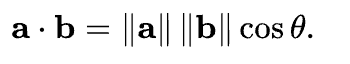
给定两个属性向量，A和B，其余弦相似性θ由点积和向量长度计算出：

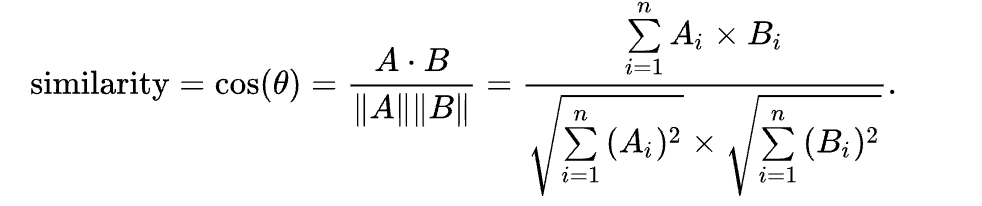
Pytorch代码：

1
2
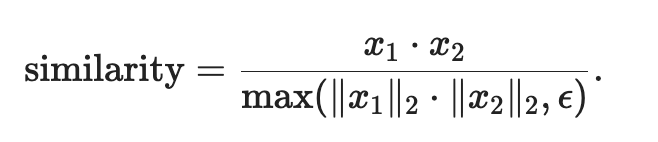
3

#given x1 and x2
cos = torch.nn.CosineSimilarity(dim=1,eps=1e-8) #eps防止分母除到0
output = cos(x1,x2)

感知相似性（Perceptual Similarity）

LPIPS：来源于CVPR2018的一篇论文《The Unreasonable Effectiveness of Deep Features as a Perceptual Metric》，该度量标准学习生成图像到Ground Truth的反向映射强制生成器学习从假图像中重构真实图像的反向映射，并优先处理它们之间的感知相似度，更符合人类的感知，可以用于衡量两个图片之间的相似度。

计算方法：

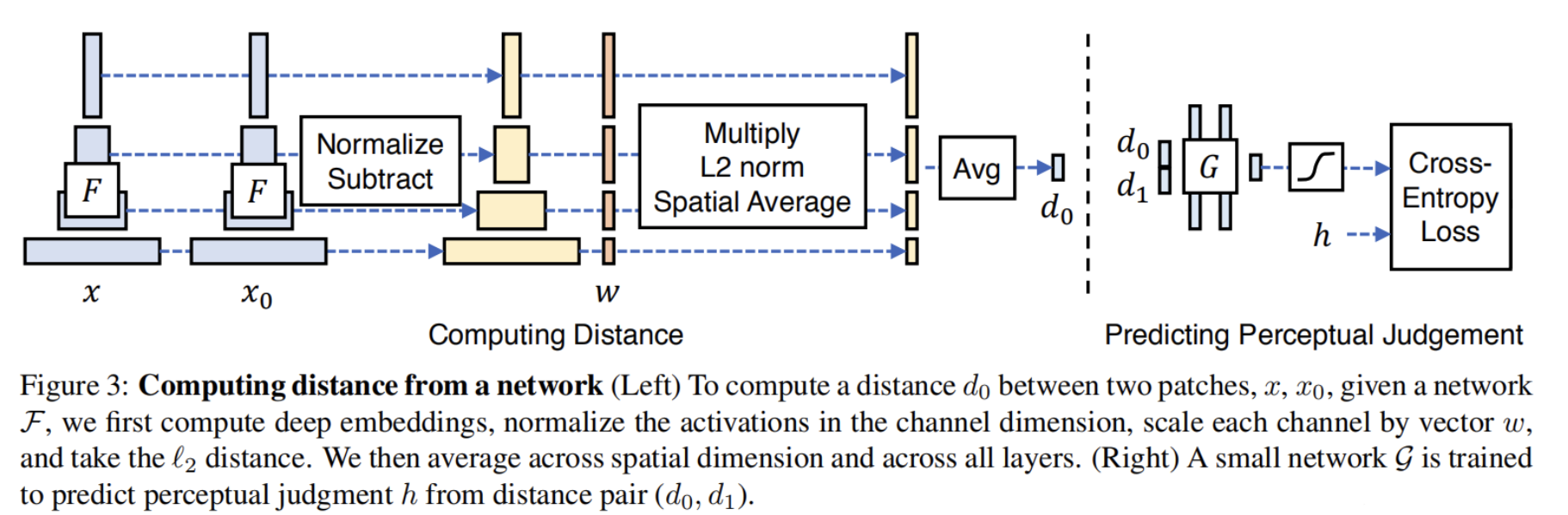
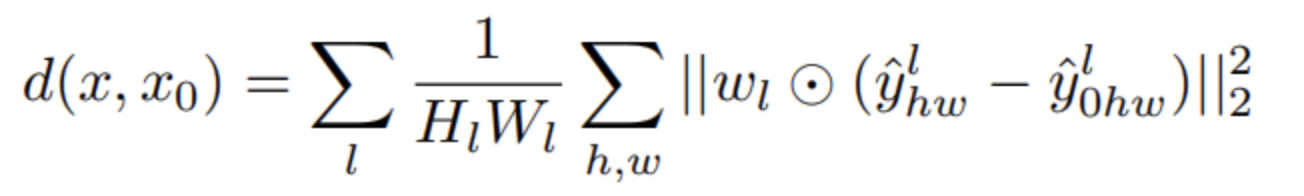
通过对各通道加和，空间平均每一层网络输出的特征图之间的距离。然后将得到的两个距离输入到评分网络中。$W_l$是与通道数同维度的可训练权重参数。其中$F$表示预训练特征提取模型，如Vgg，Alex等。

Pytorch代码：

#!pip install lpips
import lpips
lpips_fn = lpips.LPIPS(net='vgg')
output = lpips_fn(x1,x2)