Diffusion model之DDPM
本文理论公式等不做详细推导,只做总结(
毕竟是给我自己看的,不是),代码部分会详细解析。
Denoising Diffusion Probabilistic Model
前向过程: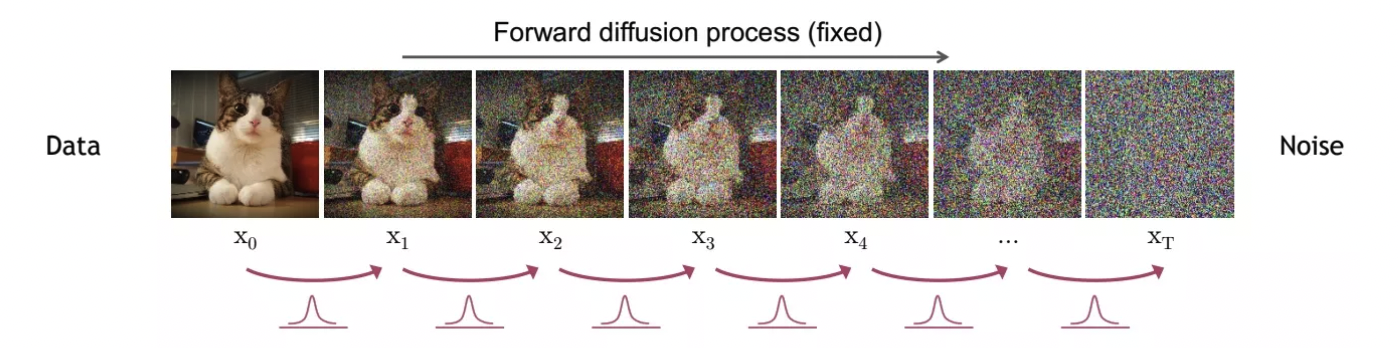
通过从原始数据分布 $\mathbf{x}_0 \sim q(\mathbf{x}_0) $ 不断加高斯噪声,根据马尔可夫链的性质,在T趋于∞的时候可以使其成为一个平稳分布(标准高斯分布) $\mathbf{x}_T \sim \varphi(\mathbf{x})$即 $X \sim N(0,1)$ ,加噪的方差(可以理解为噪声的尺度)由 $\beta_t$控制,调节上一时刻的数据和加入噪声的比例,且随时间步T变化而变化。
每个时刻加噪后的分布可以表示为 $q(\mathbf{x}_{t}|\mathbf{x}_{t-1}) := \mathcal{N}(\mathbf{x}:\sqrt{1-\beta_t}\mathbf{x}_{t-1}),\beta_tI) $,整个扩散过程可以表示为:$q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right):=\prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)$。但一步一步加噪是否可以优化,考虑是否可以一步到位,于是便可以根据正态分布的可加性继续推导,用每一个时刻的上一时刻展开表示,其中做一个表示上的代换( $\alpha_t = 1-\beta_t$ ),最后可以发现规律:
即 $q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)=\mathcal{N}\left(\mathbf{x}_{t} ; \sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0},\left(1-\bar{\alpha}_{t}\right) \mathbf{I}\right)$ ,从而我们可以一步生成任意时刻的图像:
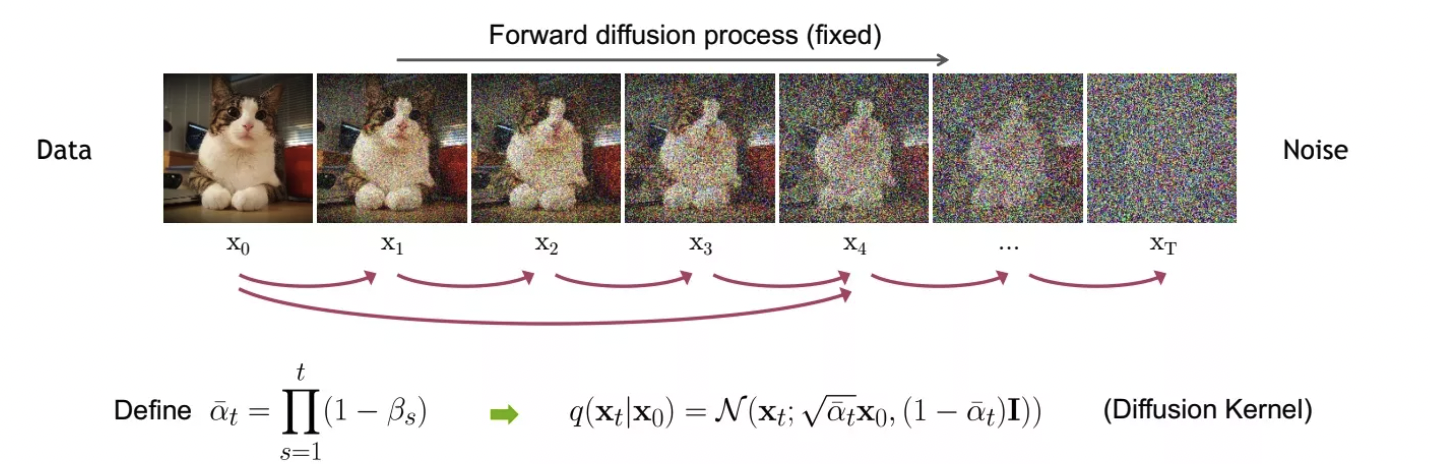
生成 $\mathbf{x}_{t}$的过程我们可以利用重参数化技巧得到。
逆向过程: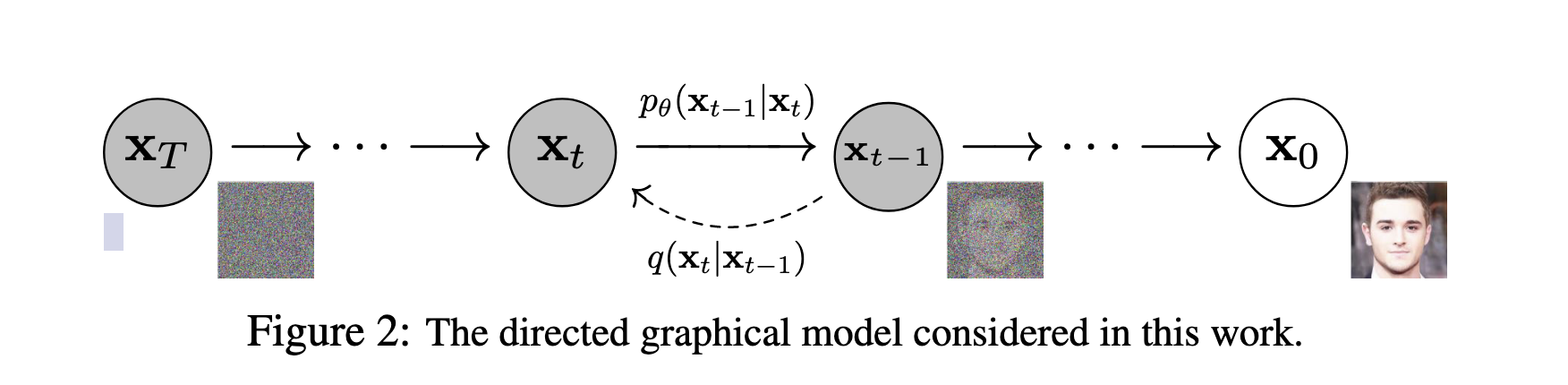
逆向是一个去噪的过程,从一个随机高斯噪声开始,一步一步生成原始高清的图片,反向过程也定义为一个马尔可夫过程,要求 $t=0$时刻的数据,即要求 $p_\theta (\mathbf{x}_{0:T}) = p\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$,但这里是 $p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)$ 我们是无从得知。
这里我们利用贝叶斯公式进行一个展开:
带入正态分布的概率密度函数,展开并配方:
配方后可以用一个新的分布表示:
其中:
其中方差可以看出是一个定值,而均值和 $\mathbf{x}_t$、$\mathbf{x}_0$有关,$\mathbf{x}_t$是已知输入,$\mathbf{x}_0$可以由前向过程一步加噪的式子代入化简。
这里我们如果我们有这个均值和方差,便可以根据这两个参数从正态分布中采样出一个数据,即得到 $\mathbf{x}_{t-1}$。但是我们没有噪声 $\boldsymbol{\epsilon}$的信息,现在可以考虑用一个神经网络$\boldsymbol{\epsilon}_\theta$ 去学习这个$\boldsymbol{\epsilon}$的信息,也可以直接学习均值的信息(但论文实验表明直接预测均值效果不好)。于是考虑用一个conditional的Unet去预测,$\boldsymbol{\epsilon}_\theta = U net(\mathbf{x}_t,t)$,之后便可以从$\mathbf{x}_t$预测得到$\boldsymbol{\epsilon}$,进而Sample出$\mathbf{x}_{t-1}$,直到$\mathbf{x}_0$
训练过程:

- 首先从我们的数据分布中sample出一个batch的数据 —> B x C x H x W
- 然后对整个batch分配从均匀分布中随机采样出的t —> B x 1 (每个样本的t不是相同的)
- 从标准正态分布中采样一个噪音,根据噪音和 $\mathbf{x}_{0}$利用公式直接生成 $\mathbf{x}_{t}$
- 根据生成的$\mathbf{x}_{t}$和$t$利用Unet预测一个噪音,和初始sample的噪声计算MSE loss
- 根据梯度优化Unet参数。
采样过程:

- 从标准正态分布中采样一个噪声作为 $\mathbf{x}_{T}$
- 执行T步循环:输入当前t和 $\mathbf{x}_{t}$,得到预测的 $\boldsymbol{\epsilon}_\theta$,根据公式计算均值和方差(DDPM里是固定的),然后从新的分布中利用重参数技巧重新采样获得上一时刻 $\mathbf{x}_{t-1}$。直到 $t=1$时结束。
代码解析:
这里对Lucidrains大佬复现的Pytorch版DDPM代码进行分析。(
简直是优雅)
代码分析顺序:
模型结构:
Unet:用于预测
noise,是带有Conditional的Unet(x,t),通过self-attention模块把Position Embedding后的时间步$\mathbf{T}$融合到Unet中,从而能更好对于不同时刻的 $\mathbf{X}_T$进行噪声的预测。训练后模型保存的就是这块的参数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87class Unet(nn.Module):
def __init__(
self,
dim,
init_dim = None,
out_dim = None,
dim_mults=(1, 2, 4, 8), ##对应Unet下采样4个阶段通道数的变换,数值对应变化的倍数
channels = 3, ##输入图像的通道数
self_condition = False, ##控制Unet中是否加入自注意力机制。
resnet_block_groups = 8,
learned_variance = False,
learned_sinusoidal_cond = False,
random_fourier_features = False,
learned_sinusoidal_dim = 16
):
super().__init__()
# determine dimensions
self.channels = channels
self.self_condition = self_condition
input_channels = channels * (2 if self_condition else 1)
init_dim = default(init_dim, dim) ##init_dim有定义则设置为init_dim,无就默认dim
self.init_conv = nn.Conv2d(input_channels, init_dim, 7, padding = 3)
dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
block_klass = partial(ResnetBlock, groups = resnet_block_groups)
# time embeddings
time_dim = dim * 4
self.random_or_learned_sinusoidal_cond = learned_sinusoidal_cond or random_fourier_features
if self.random_or_learned_sinusoidal_cond:
sinu_pos_emb = RandomOrLearnedSinusoidalPosEmb(learned_sinusoidal_dim, random_fourier_features)
fourier_dim = learned_sinusoidal_dim + 1
else:
sinu_pos_emb = SinusoidalPosEmb(dim) ##正弦位置编码
fourier_dim = dim
self.time_mlp = nn.Sequential( ##对步长进行一个编码和转换的MLP
sinu_pos_emb,
nn.Linear(fourier_dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
# layers
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
##堆叠下采样残差块
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(nn.ModuleList([
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
Downsample(dim_in, dim_out) if not is_last else nn.Conv2d(dim_in, dim_out, 3, padding = 1)
]))
mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
##堆叠下采样残差块
for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
is_last = ind == (len(in_out) - 1)
self.ups.append(nn.ModuleList([
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
Upsample(dim_out, dim_in) if not is_last else nn.Conv2d(dim_out, dim_in, 3, padding = 1)
]))
default_out_dim = channels * (1 if not learned_variance else 2)
self.out_dim = default(out_dim, default_out_dim)
self.final_res_block = block_klass(dim * 2, dim, time_emb_dim = time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
- GassianDiffusion:将整个diffusion process和reverse diffusion集成在一起的类,载入了Unet模型。可以进行任意时间步的扩散,以及单步采样和整个时间步长的采样循环。同时提供了训练时计算Loss的过程,整个
forward过程返回的就是训练的Loss。
训练过程:
看decoder后分类变不变,或者latent diffusion后分类变不变
ldm换l1,unet通道倍数1,2,2,2
ae的训练encode,只在encoder里除10.